本试卷总分100分,考试时间150分钟。
一、单项选择题(每小题2分,共40分)
1.设函数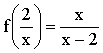 ,则f(2x)=( )
,则f(2x)=( )
A.
B.
C.
D.
2.当x→+∞时,下列函数为无穷大量的是( )
A.
B.
C.
D.
3.下列函数中,在x=0处不连续的是( )
A.
B.
C.
D.
5.曲线y=3+lnx在点(1,3)处的法线方程为( )
A.x+y-4=0
B.x+y+4=0
C.3x-y=0
D.4x-y-1=0
9.函数f(x)=![]() 的单调增区间为( )
的单调增区间为( )
A.(-∞,4]∪[12,+∞)
B.(-∞,-12]∪[-4,+∞)
C.[4,12]
D.[-12,-4]
14.在空间直角坐标系中,动点P到定点A与到定点B的距离相等,则动点P的轨迹是( )
A.直线
B.圆
C.平面
D.球面
12.下列广义积分收敛的是( )
A.
B.
C.
D.
15.已知函数z=![]() ,则
,则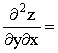 ( )
( )
A.
B.
C.
D.
10.不定积分 ( )
( )
A.
B.
C.
D.
16.函数z=f(x,y)在点(x0,y0)处( )
A.可导一定可微
B.可微一定可导
C.可导一定不可微
D.可微一定不可导
17.设G是由曲面x^2+y^2=R^2及z=0,z=1所围成的积分区域,则三重积分![]() 在柱面坐标下的累积分为( )
在柱面坐标下的累积分为( )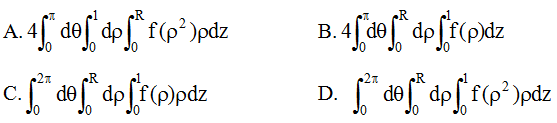
A.
B.
C.
D.
19.下列幂级数中,收敛半径R=3的幂级数是( )
A.
B.
C.
D.
4.设f(x)在x0处可导,则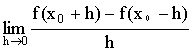 =( )
=( )
A.
B.
C.
D.
11.函数在f(x)=x^2+1在[1,3]上的平均值为( )
A.16/3
B.7/3
C.32/3
D.9
18.下列级数中,条件收敛的是( )
A.
B.
C.
D.
13.点(2,3,-1)到平面2x-3y+z-6=0的距离为( )
A.
B.
C.
D.
20.微分方程y"-2y'+1=0的通解y=( )
A.
B.
C.
D.
6.设函数y(x)=f(cos![]() ),其中f(x)为可导函数,则
),其中f(x)为可导函数,则![]() ( )
( )
A.
B.
C.
D.
7.设函数y=f(x)有f'(0)=2,则当![]() 时,f(x)在x=0处的微分dy是( )
时,f(x)在x=0处的微分dy是( )
A.比△x高阶无穷小
B.比△x低阶无穷小
C.与△x同阶无穷小,但不是等价无穷小
D.与△x等价无穷小
8.设函数f(x)在x0点满足f'(x0)=f"(x0)=0,则f(x)在x0处( )
A.有极大值
B.有极小值
C.无极值
D.可能有极值,也可能没有极值
二、填空题(每小题2分,共20分)
1.极限 =______.
=______.
3.设参数方程 确定函数y=y(x),则
确定函数y=y(x),则![]() ______.
______.
9.当|x|<![]() 时,函数f(x)=
时,函数f(x)=![]() 的x幂级数展开式为______.
的x幂级数展开式为______.
6.定积分![]() ______.
______.
10.微分方程xy'+y=x的通解为______.
4.不定积分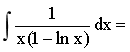 ______.
______.
7.设函数z=ln(3x+2y),则dz______.
2.极限![]() =______.
=______.
5.![]() ______.
______.
8.设L是曲线y=x^2从(0,0)到(1,1)的一段弧,则曲线积分![]() ______.
______.
三、计算题(每小题5分,共25分)
1.设函数f(x)=2^x+x^2+x^x,求f'(x).
5.判断级数1-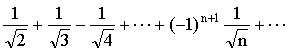 的敛散性.
的敛散性.
2.设函数f(x)=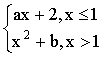 在x=1处可导,求常数a和b.
在x=1处可导,求常数a和b.
4.设B是由曲线y=![]() 及x=2所围成的积分区域,求二重积分
及x=2所围成的积分区域,求二重积分![]() .
.
3.设函数f(x)=![]() ,求
,求![]() .
.
四、应用和证明题(每小题5分,共15分)
1.证明:当x>1时,有e^x>ex成立.
2.求由曲线y=x^2,y=2x^2及y=1所围第一象限的平面图形的面积.
3.求抛物面z=3x^2+2y^2在点(2,-1,14)处的切平面方程.

