本试卷总分100分，测试时间150分钟。

一、单项选择题（每小题3分，共15分）

1.(      )

A.
B.
C.
D.

3.设F（x,y）具有连续的偏导数，且xF(x,y)dx+yF(x,y)dy是某函数u(x,y)的全微分，则（      ）

A.
B.
C.
D.

2.设积分区域Ω：,则三重积分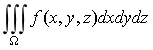，在球坐标系中的三次积分为（      ）

A.
B.
C.
D.

4.微分方程的一个特解应设为y*=（      ）

A.
B.
C.
D.

5.下列无穷级数中，发散的无穷级数为（      ）

A.
B.
C.
D.

一、填空题(本大题共5小题，每空2分，共10分)

1.点P(0,-1,-1)到平面2x+y-2z+2=0的距离为_____________。

2.设函数,则=_____________。

3.设∑为球面,则对面积的曲面积分_____________。

4.微分方程的通解 y= _____________。

5.设函数 f(x) 是周期为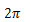的函数, f(x)的傅里叶级数为 ，则傅里叶级数b₃= _____________。

三、计算题（每小题5分，共60分）

1.求过点P(2,-1,3),并且平行与直线的直线方程.

2.设函数f(x,y)=(1+xy)^x,求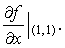

5.求抛物面

6.计算二重积分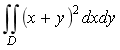,其中积分区域D:

7.计算三重积分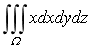,其中积分区域Ω是由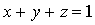及坐标面所围成区域.

3.设函数,求全微分dz.

8.计算对弧长的曲线积分  其中C是y=3-x上点A(0,3)到点B(2,1)的一段.

4.设函数z=f(e^(xy),y),其中f(u,v)具有一阶连续偏导数,求.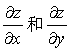

9.计算对坐标的曲线积分,其中C是摆线上点A(0,0)到点B(2π,0)的一段弧.

12.将函数展开为x的幂级数.

10.求微分方程

11.判断无穷级数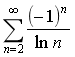的敛散性.

四、综合题（每小题5分，共15分）

1.求函数的极值.

3.证明无穷级数  收敛,并求其和.

2.计算由曲面三个坐标面及平面x+y=1所围立体的体积.